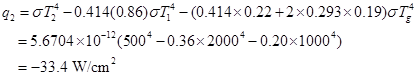If all surface temperatures are specified in a problem, the results from Eq. (A-17) complete the solution. If qk is specified for n surfaces and Tk for the remaining N–n surfaces, then the n unknown surface temperatures are guessed, the equations are solved for all q, and then the calculated qk are compared to the specified values. If they do not agree, new values of Tk for the n surfaces are assumed and the calculation is repeated until the given and calculated qk agree for all Ak with specified qk. Equation (11-8), expressed as a sum over the wavelength bands, gives the required energy input to the medium for the specified Tg.

 

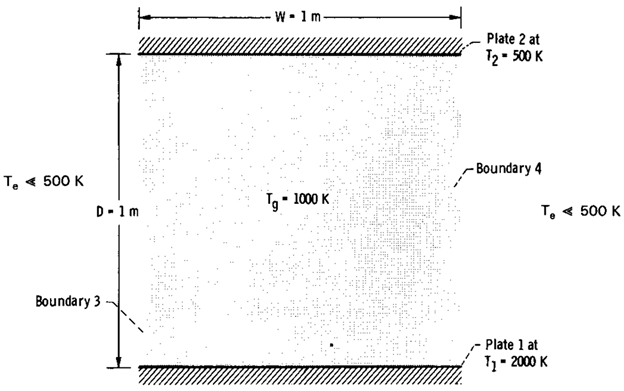
EXAMPLE A-2 Two black parallel plates are D = 1 m apart. The plates are of width W = 1 m and have infinite length normal to the cross section shown (Fig. A-9). Between the plates is carbon dioxide gas at  atm and Tg = 1000 K. If plate 1 is at 2000 K and plate 2 is at 500 K, find the energy flux that must be supplied to plate 2 to maintain its temperature. The surroundings are at Te << 500 K.

 

A006x009
FIGURE A-9 Example A-2 Figure

 

As shown by Fig. A-9, the geometry is a four-boundary enclosure formed by two plates and two open planes. The open areas are perfectly absorbing (nonreflecting) and radiate no significant energy as the surrounding temperature is low. The energy flux added to surface 2 is found by using the enclosure equation (10-72) where k = 2 and N = 4. All surfaces are black, ελ,j = 1, so Eq. (10-72) reduces to

 

                        (A-18)

 

The self-view factor F2–2 = 0 and Eλb,3 = Eλb,4 ≈ 0, so this becomes

 

           (A-19)

 

To simplify the example, it is carried out by considering the entire wavelength region as a single spectral band. To obtain the total energy supplied to plate 2, integrate over all wavelengths to obtain

 

 

By use of the definitions of total transmission and absorption factors,

 

 

and so forth, q2 becomes

 

                 (A-20)

 

To determine  and , the geometric-mean beam length is used. For opposing rectangles (Fig. A-8) at an abscissa of 1.0 and on the curve for a length-to-spacing ratio of ∞, the , so . To determine , which determines the emission of the gas, use the Lechner correlation (9-62) or Fig. 9-15) at a pressure of 1 atm, Le = 1.34 m (giving pLe = 138 bar-cm) and Tg = 1000 K. This gives . When obtaining , note from (A-19) that the radiation in the  term is Eλb,1 and is coming from wall 1. Therefore it has a spectral distribution different from that of the gas radiation. To account for this nongray effect, (10-118) is used with ε+ evaluated at =277 bar-cm and T1 = 2000 K. Then, using the Lechner correlation or Fig. 9-15 (extrapolated) and Eq. (10-118) result in .

 

From factor 3 in Appendix C the F2–1 is given by . Then . The , and they remain to be found. For adjoint planes, as in the geometry for Table 12-2, the following expression from Eq. (12) of Dunkle (1964) can be used, obtained for the present case where b →∞, a = 1, and c = 1:  Using Fig. 9-15  = 77.7 bar-cm and Tg= 1000 K gives . Then the desired result is

 

 

Note that the largest contribution to q2 is by energy leaving surface 1 that reaches and is absorbed by surface 2. Emission from the gas to surface 2, and emission from surface 2, are small.

 

An alternative approach for this particular example is to note that the term involving Tg in (A-20) is the flux received by surface 2 as a result of emission by the entire gas. This can be calculated from (10-114) using the mean beam length. Then . For this symmetric geometry the average flux from the gas to one side of the enclosure is the same as that to the entire enclosure boundary. Consequently, the mean beam length can be obtained from (10-112) as  Then, from Fig. 9-15 at Tg = 1000 K and = 92.9 bar-cmthe εg = 0.20. This gives the same q2 as Previous Pagely calculated.